TLS (1) : 암호화 메커니즘

암호화(encryption)란, 특별한 지식을 소유한 사람들을 제외하고 그 누구든 읽을 수 없도록 알고리즘을 이용하여 정보를 전달하는 과정을 일컫는다. 암호화되기 전의 정보를 평문(plaintext), 암호화된 정보를 암호문(ciphertext)이라 부른다. 암호화에 역행하는 과정, 즉 암호문을 보고 평문을 얻는 과정을 복호화(decryption)이라 부른다.

대칭 키 암호

대칭 키 암호(symmetric-key algorithm)란, 암호화와 복호화에 똑같은 키(Key)를 사용하는 방식을 말한다. 키는 암호 알고리즘을 작동시키기 위한 일종의 '비밀번호'와 같다. 자물쇠를 잠글 때 사용한 열쇠가 있어야만 다시 열 수 있는 것처럼, 대칭 암호는 송신자와 수신자가 동일한 키를 공유하고 있어야 한다는 특징이 있다.

이때 암호 알고리즘의 안전성은 알고리즘 자체의 비밀이 아니라, 오직 키의 비밀성에 의존해야 한다. 누구나 원리를 알 수 있는 알고리즘이라 할지라도, 올바른 키 없이는 어떠한 수학적 방법으로도 해독할 수 없어야 훌륭한 암호 알고리즘이라 할 수 있다(이를 Kerckhoffs' Principle이라 부른다).

치환 암호

치환 암호에 해당하는 ROT13

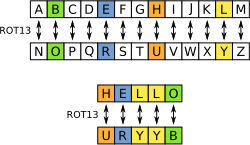
치환 암호(substitution cipher)는 대칭 암호의 일종으로, 위 그림처럼 표를 보고 원래의 문자를 그에 대응하는 다른 문자로 치환하는 암호이다. 이 암호는 영어에 자주 등장하는 알파벳을 따져보는 등 통계적 방법으로 쉽게 복호화가 가능하므로, 현대에는 사실상 사용되지 않는다.

전치 암호

전치 암호(transposition cipher)는 대칭 암호의 일종으로, 문자 위치를 뒤섞는 것을 뜻한다. 위 그림에는 20글자짜리 평문을 4x5 격자에 넣은 뒤, 열을 정해진 순서로 뒤섞고 세로로 읽는 전치 암호가 그려져 있다. 이 역시 여러 열의 순서와 격자 크기를 브루트포스하는 등의 방식으로 쉽게 풀리기 때문에, 잘 사용되지 않는다.

AES

AES(Advanced Encryption Standard)는 대표적인 대칭 암호로, 키의 길이와 라운드 수에 따라 AES-128, AES-256 등으로 분류된다. AES는 암호화를 여러 라운드에 걸쳐 진행하는데, 각 라운드에는 치환/전치 등 일련의 연산이 적용되어 평문을 점점 더 난독화한다.

이렇게 생성된 암호문은 키 없이는 복호화가 사실상 불가능할 정도로 강력하여, 오늘날의 HTTPS, VPN 등에 널리 활용되고 있다.

키 교환 문제

대칭 키 암호 방식의 가장 큰 약점은 키 교환 문제이다. 암호 통신을 시작하기 위해서는 사전에 양측이 키를 나눠 가져야 하는데, 이 과정에서 누군가 중간에 키를 가로챈다면, 아무리 강력한 알고리즘을 사용하더라도 암호문은 쉽게 해독되고 만다. 또한 키가 유출됐는지를 알 방법도 없어, 중간자 공격에 취약하다는 문제가 있다.

비대칭 키 암호

비대칭 키 암호(asymmetric-key algorithm)란, 암호화와 복호화에 서로 다른, 그러나 연관된 키를 사용하는 방식을 말한다. 이때 누구에게나 알려져 있는 키를 공개키(public key), 소유자만이 비밀리에 보관하는 키를 개인키(private key)라 부른다. 누군가 공개키로 암호화한 암호분은 개인키로만 복호화할 수 있다. 따라서 공개키를 누군가 가로채더라도 그 키로는 암호문을 복호화할 수 없으므로 키 교환 문제가 해결된다.

트랩도어 함수

f는 다항 시간 안에 쉽게 계산이 가능하지만, t가 없이 f의 역함수를 구하는 것이 어려울 경우에 f를 trapdoor function이라 한다.

비대칭 키 암호는 트랩도어 함수(trapdoor function)에 의존한다. 트랩도어 함수란, 한 방향으로는 계산하기 쉽지만 비밀 정보(trapdoor)를 알지 못하면 반대쪽 방향으로는 계산이 어려운 함수를 뜻한다. 비대칭 키 암호에서는 트랩도어 함수를 계산할 수 있는 정보를 공개키로, 함수를 역산하여 원래대로 되돌릴 수 있는 핵심 정보인 트랩도어를 개인키로 사용한다.

RSA 암호

RSA(Rivest-Shamir-Adleman)는 대표적인 트랩도어 함수인 '큰 수 소인수분해'에 기반을 둔 비대칭 키 암호이다. 

컴퓨터로 두 개의 큰 소수 p와 q를 곱하여 하나의 수 N을 구하는 것은 순식간에 계산 가능하다. 하지만 반대로, 결과값 N을 보고 원래의 두 소수 p와 q를 찾아내는 소인수분해는 수가 커질수록 천문학적인 시간이 소요되어 사실상 불가능에 가깝다. 이때 곱셈의 결과인 N이 누구나 알 수 있는 공개키의 일부가 되며, 원래의 소수 p와 q는 개인키를 생성하는 핵심 정보, 즉 트랩도어가 된다. 해커가 공개키를 획득하더라도 이를 소인수분해하여 개인키를 찾아내는 것은 현재의 컴퓨팅 능력으로는 불가능하다는 원리를 이용한 것이다.

RSA는 오랜 기간 검증된 안전성으로 인해 오늘날 HTTPS, SSH 접속 등 보안이 필요한 거의 모든 인터넷 인프라에 활용되고 있다.

---

출처

<한 권으로 읽는 컴퓨터 구조와 프로그래밍>, 13장

https://en.wikipedia.org/wiki/ROT13

https://en.wikipedia.org/wiki/Trapdoor_function

https://blog.naver.com/wnrjsxo/221705557143